本文采用模因技术形式的混合正弦余弦算法(SCA)来解决电力工程中的一个重要问题——经济负荷调度问题。ELD是通过分配一组具有最低燃料成本的发电机组来解决的，这些发电机组根据一组相等和不相等约束来产生预定义的负载需求。SCA是一个最新的基于种群的优化器，它使用基于正弦和余弦三角函数的基于数学的模型来实现最优解决方案。与其他优化方法一样，SCA在求解像ELD这样的非线性约束问题时，在开发过程中存在主要缺陷。因此，\(\beta \)爬坡优化器作为一种最新的局部搜索算法，在SCA中被混合为一个新的操作符，以增强其处理ELD的开发能力。所提出的混合算法缩写为SCA-\(\beta \)HC，使用两组现实世界的发电案例进行评估:(i) 3单元，13单元和40单元的两个版本，忽略斜坡速率限制和禁止操作区域约束。(ii)设有斜坡速率限制和禁止操作区域限制的6个和15个单元。初步研究了SCA-\(\beta \)HC控制参数的灵敏度分析。结果表明，通过将SCA-\(\beta \)HC算法的参数调整到合适的值，可以提高算法的性能。与几种最先进的方法的比较评价表明，所提出的方法能够对某些测试案例产生新的最佳结果，而对其他测试案例产生次优结果。简而言之，杂交\(\beta \)HC优化器作为SCA的新算子是解决ELD问题的非常强大的算法。

经济负荷调度是电力系统领域的非劳动优化问题。它关注的是在功率平衡相等约束和功率输出不相等约束下，以最小的总燃料成本满足特定运行时期的发电负荷需求，有时会有斜坡速率限制和禁止运行区域。ELD已被表述为具有非线性、非凸约束特征的优化问题，这些特征不容易被基于微积分的方法操纵(El-Keib等人，1994;Panigrahi et al. 2012;Chen and Ding 2015)。因此，近似和约束处理是解决这类问题最成功的技术。

ELD密集使用的近似方法之一是基于元启发式的方法(al - betar et al. 2018b)。元启发式是一种通用的优化模型，可适用于各种优化问题。由于初始解的数量，元启发式分为两大类:基于群体的算法和基于局部搜索的算法(Blum和Roli 2003)。基于种群的算法在探索方面非常强大，而在利用方面很弱。相反，基于局部搜索的方法在开发方面非常强大，而在探索方面很弱(al - betar et al. 2014)。为了补充种群和局部搜索方法的优势，在开发和勘探过程之间提供适当的权衡，通常建议采用混合机制(Blum et al. 2011)。这种杂交被称为模因算法(MA)。在MA中，以模因为代表的局部搜索算法中的文化选择机制与以基因为代表的基于种群的框架中建立的自然选择原则相结合(Ong和Keane 2004)。模因的行为就像文化进化中的一个局部/个人改进代理。基因和模因都反映了普遍性(基因)和问题特异性(模因)的自然和文化选择(Ong et al. 2006;al - betar et al. 2014)。

最近建立了基于人口的元启发式算法，称为正弦余弦算法(SCA)，利用正弦和余弦三角函数特征来更新解决方案(Mirjalili 2016b)。与其他基于种群的算法相比，它有一个显著的特点:首先，它在初始搜索中没有衍生值，因此新手优化用户可以很容易地使用它。其次，它具有智能算子，可以利用适者生存的原则，通过正弦和余弦三角函数迭代积累特定问题的知识。简而言之，它的概念简单，收敛性强，易于用于任何问题，健全而完整。因此，SCA已被广泛应用于许多优化问题，如最优潮流(Attia等人，2018)、特征选择(Sindhu等人，2017)、短期热液调度(Das等人，2018)、目标跟踪(Nenavath等人，2018)、图像分割(Oliva等人，2018)、机组承诺问题(Reddy等人，2018)、自动电压调节系统(Hekimo?lu 2019)、电力系统负荷裕度稳定性(Mahdad和Srairi 2018)、壳管式蒸发器的优化设计(Turgut 2017)、病脑检测(Nayak et al. 2018)、弯曲光子晶体波导的设计(Mirjalili et al. 2020)、无线传感器节点定位器(Hamouda and Abohamama 2020)、突然运动跟踪(Zhang et al. 2020)、径向配电系统中分布式发电机的优化分配(Raut and Mishra 2020)、非线性双层规划问题(Abo-Elnaga and El-Shorbagy 2020)、旅行推销员问题(Tawhid and Savsani 2019)、桁架结构(Gholizadeh and Sojoudizadeh 2019)、训练多层感知器(Gupta and Deep 2020)、支持向量回归的参数优化(Li et al. 2018)、文本分类(Belazzoug et al. 2019)等。

SCA与其他基于群体的算法一样，在处理具有组合性质和约束特征的现实优化问题时，需要仔细修改或与其他启发式算法的强组件杂交以提高其性能(Gupta和Deep 2019a)。因此，SCA的几个修改版本，例如:(i)与基于本地的算法混合(Chen et al. 2019;Liu et al. 2019;Tawhid and Savsani 2019)， (ii)与其他基于种群的算法杂交(Nenavath and Jatoth 2018;Chegini et al. 2018)， (iii)与借鉴其他优化算法的其他算子杂交(Liu et al. 2019;Gupta和Deep 2019b)，以及(iv)修改其操作人员以符合问题性质(Gupta和Deep 2019a;Sindhu et al. 2017;Long et al. 2019;Chen et al. 2020)。特别地，SCA与高斯局部搜索和随机突变相结合，以增强种群的多样性(Liu et al. 2019)。Long et al.(2019)引入了一种新的基于高斯函数的非线性转换参数，以在勘探和开采之间取得适当的平衡，并提出了一种改进的位置更新方程，以加速收敛并避免局部最优问题。在另一项研究中，SCA与Nelder-Mead单纯形概念和基于对立的学习方案相结合(Chen et al. 2019)。在该方法中，利用Nelder-Mead单纯形概念来增强种群的开发，利用基于对立的学习方案来提高种群的多样性。

如前所述，为了提高SCA处理具有约束特征的ELD问题的性能，可以将一种成功的基于局部搜索的算法与SCA优化框架混合作为新的算子，从而利用模因和基因的概念。最近由Al-Betar(2017)提出的基于局部搜索的算法被称为爬山(HC)优化器。

原则上，HC优化器是一种基于局部搜索的算法，由单个解启动。迭代地，使用两个操作符将该解移动到它的邻近解:-操作符用于邻近搜索，-操作符用于探索。贪心选择机制用于当前解和相邻解之间的竞争。这个过程不断重复，直到满足停止条件。该算法的主要优点是简单易用。通过其导航搜索空间和逃避局部最优的机动行为，HC优化器已成功地定制并与其他基于种群的算法杂交，用于许多优化问题，如检查时间表(al - betar 2021)，特征选择(Ghosh等人，2020)，心电和脑电图信号去噪(Alyasseri等人，2018,2017)，生成替换框(Alzaidi等人，2018)，基因选择(Alomari等人，2018b)，经济负荷调度问题(al - betar et al. 2018a)、多水库调度问题(Alsukni et al. 2019)、数独游戏问题(al - betar et al. 2017)、文本文档聚类问题(Abualigah et al. 2017a, b)、分类问题(Alomari et al. 2018a;Alweshah et al. 2020)，以及数学优化函数(Abed-alguni and Alkhateeb 2020)。使用HC作为模因的主要动机是它具有深入挖掘基于种群的算法所达到的搜索空间区域的特性。通过-算子，HC利用当前解的特征并移动到邻近解。另一方面，通过-算子，HC可以使用一致突变策略逃避局部极小值。HC的主要限制是参数整定，使用HC的研究需要研究其控制参数的合适值。

本文将SCA作为基因因子与HC作为模因因子进行杂交，解决了经济负荷调度问题。这是为了增强SCA处理ELD问题的性能。所提出的混合算法缩写为SCA-HC，使用两组现实世界的发电案例进行评估:(i) 3单元，13单元和40单元的两个版本，忽略斜坡速率限制和禁止操作区域约束。(ii)设有斜坡速率限制和禁止操作区域限制的6个和15个单元。初步研究了SCA-HC控制参数的敏感性分析，以显示其对所提出的SCA-HC算法的影响。对比评价表明，SCA-HC能够有效地解决ELD问题。综上所述，SCA-HC算法对于诸如ELD这样的电力系统是一种成功的算法。

本文的其余部分组织如下:根据第2节中的优化方法定义和表述ELD问题。建议的方法在第3节中提出。此后，在第4节中提供了所有真实世界测试用例的比较评估的结果和讨论。最后，结论与建议的未来方向给出了在第5节。

在优化环境下建立经济负荷调度问题的模型，通过在相等约束和不相等约束下为每台发电机组分配最小的燃料成本来产生恒定的负荷需求。在本节中，给出了ELD的数学表达式。然后，对以往的ELD方法进行了讨论。

ELD可以被表述为一个具有挑战性的优化问题，它可能是许多优化技术的有价值的目标。与任何优化问题一样，这类问题的目标函数都需要制定，以反映优化技术可以利用的精确数学模型。

这里考虑的ELD问题有N个发电机组，每个机组可以使用的燃料成本范围不同。这里的目标是为每个单元分配适当的允许燃料成本，从而使所有单元的总燃料成本最小。优化必须满足一组约束条件，使最优解始终是可行的。在下面的章节中，给出了ELD问题的主要优化项的数学表达式。

ELD的解的表示是用向量空间表示的。它被表示为一个向量，其中，是发电单元号i，它将取一个值范围。的值指的是下界，而指的是上界。

用燃料成本来评价ELD解的目标函数如式(1)所示。

（1)

式中为N台的总燃料成本，是计算每台燃料成本的函数。单位燃料成本计算如式(2)所示。

（2）

光滑系数()和非光滑系数()与单元i有关。正弦函数表示阀点负载获得的波在热速率趋势中的影响。这揭示了避免陷入局部最优解的更多挑战(Alsumait et al. 2010)。

在每个ELD解决方案中，应满足两个主要约束和两个扩展约束，以确保ELD解决方案的可行性。在接下来的部分中，这些约束是用数学公式表示的。

2.4.1 等式约束

第一个约束是系统总发电量与系统总负荷之间的平衡功率，其功率损耗在数学上如式(3)所示。

(3)

式中，系统的传输损耗用发电出力的二次函数表示，如式(4)所示。

（4）

式中，为损耗系数矢量的元素，为元素的损耗系数平方。在文献中(Cai et al. 2012b;Alsumait et al. 2010;Cai et al. 2012a;Lin et al. 2011;Tsai et al. 2011)，通过考虑传输损耗来简化。

2.4.2 不等式约束

等式约束是第二个约束，它规定了发电单元的上、下取值范围()，计算如式(5)。

(5）

2.4.3 斜坡速率限制

不等式约束有时受到斜坡速率限制的限制。它发生在两个操作周期之间。单元生成的过程将增加或减少。这是根据上坡率和下坡率周期完成的，形式化如下:

增加发电量受到以下限制:

减小发电量的约束条件为:

其中，为机组1的前一个发电时段，分别表示斜坡速率上限和斜坡速率下限。因此，不等式约束通过斜坡速率限制进行调整，如下所示:

2.4.4 禁止操作区域

由于机器部件的物理限制或轴轴承振动引起的不稳定性，发电机组可能受到禁止操作区域的限制。这将导致可以检测到的成本波动。因此，与禁止操作区域相对应的成本曲线将出现不连续性。避免在这些地区作业将导致节约生产。形式上，对于发电机组i，

注意，和分别表示发电机组i的给定禁区的下限和上限。

最后，在ELD问题中考虑禁作区约束的情况下，燃料成本如式(6)所示。

(6）

式中为操作区域约束的处罚因子，(违例)为进入禁止操作区域的指标(Safari and Shayeghi 2011)。

最近介绍了几种基于元启发式的算法。这些算法在很多情况下模仿生物的自然行为，如人类、动物和植物。基于元启发式的算法是一般的优化算法。它们跨越整个搜索空间，并使用智能运算符来调整可行的解决方案。他们使用精心选择的参数值来提出最佳解决方案(Blum和Roli 2003)。最近基于元启发式算法的例子有Seeker优化算法(Dai等人，2006)、蜻蜓算法(Mirjalili 2016a)、冠状病毒群体免疫优化器(al - betar等人，2020a)、多元空间优化器(Mirjalili等人，2016)、蚂蚁狮子优化器(Mirjalili 2015a)、哈里斯鹰优化(Heidari等人，2019)、蛾焰优化算法(Mirjalili 2015b)、乌鸦搜索算法(Askarzadeh 2016)、正弦余数算法(Mirjalili 2016b)、蚱蜢优化算法(Saremi et al. 2017)，鲸鱼优化算法(Mirjalili and Lewis 2016)，以及(Fausto et al. 2020)中报道的许多其他算法。它们通常分为:基于单一解决方案的方法和基于人口的方法(Boussa?D et al. 2013)。

依赖于从单一状态开始的解决方案，从一个随机解决方案开始，并不断更新和修改该解决方案，从一个状态移动到另一个状态，直到达到称为“局部最小值”的稳定状态。这些方法通常以类似于深度优先方法的轨迹形式深度跨越搜索空间，但缺乏广泛的搜索机制。解决ELD的一些解决方案包括模拟退火(Wong and Fung 1993)、GRASP (Neto et al. 2017)、爬坡(al - betar et al. 2018a)和禁忌搜索(Lin et al. 2002)。

另一方面，基于群体的方法从随机解决方案(个体)的群体开始，并行地扫描所有可能的解决方案。他们交换零碎的信息，并使用一定程度的随机性来更具创造性和剥削性。这些技术具有同时扫描广泛搜索空间区域的能力，但它不能严格地导航扫描区域以找到它们的局部最优(Blum和Roli 2003)。几种基于种群的方法用于求解ELD，如粒子群优化(Qin et al. 2017;Jain等人，2018)，蚁群优化器(Pothiya等人，2010)，布谷鸟搜索算法(Basu和Chowdhury 2013)，萤火虫算法(Sinha等人，2003)，磷虾群算法(Mandal等人，2014)，人工蜂群(Hemamalini和Simon 2010)，花授粉算法(Shilaja和Ravi 2017)，社交蜘蛛算法(James和Li 2016)，乌鸦搜索算法(Mohammadi和Abdi 2018)，人工藻类算法(Kumar和Dhillon 2018)，蛾火焰算法(Tripati等人，2018);Elsakaan et al. 2018)， Fireworks Algorithm (Jadoun et al. 2018;Pandey et al. 2018)、和谐搜索算法(Pandi et al. 2011)、蚂蚁狮子优化器(Kamboj et al. 2017)、蜻蜓算法(Suresh and Sreejith 2017)、遗传算法(Subbaraj et al. 2011)、环境适应方法(Sharma et al. 2017)和基于生物地理的算法(Bhattacharya and Chattopadhyay 2010a)。

为了构建一种高效的搜索机制，我们需要将两种搜索方法混合起来;基于单解的搜索方法和基于种群的搜索方法。当我们杂交时，我们期望收获两种方法的优点(Blum和Roli 2003)。我们期望有一种除广泛搜索外还能进行深度搜索的算法，并伴随着智能信息交换算子和适者生存选择机制。用于求解ELD的最成功的混合技术如下:

1. 1.

   序列二次规划与差分进化相结合(Elaiw et al. 2013)。

2. 2.

   序列二次规划与粒子群优化相结合(Victoire and Jeyakumar 2004;Elaiw et al. 2013)。

3. 3.

   遗传算法与shuffledfrog jumping Algorithm (Roy et al. 2013)相结合。

4. 4.

   将二次规划与混沌微分进化相结合(Coelho and Mariani 2006)。

5. 5.

   细菌觅食方法与遗传算法相结合(Elattar 2015)。

6. 6.

   粒子群优化与差分进化相结合(Parouha and Das 2016)。

7. 7.

   GRASP算法与差分进化相结合(Neto et al. 2017)。

8. 8.

   局部搜索与人工蜂群算法(?zy?n和Aydin 2013)相结合。

9. 9.

   差异进化与化学反应优化相结合(Roy et al. 2014)。

10. 10.

    基于生物地理学的优化与差异进化相结合(Bhattacharya and Chattopadhyay 2010c)。

最近的一项研究(Le Yang 2020)提出了一种基于超启发式选择(SHHA)的算法来解决动态经济排放调度(DEED)问题。建立了包括风能、太阳能和储能在内的多目标动态经济和环境负荷分配问题的数学模型。为解决电力系统的时空耦合调度问题提供了一种新的思路。他们使用非优势排序策略来指导筛选亲本个体。他们试图将不可行的解决方案转化为可行的解决方案，以提高解决方案的质量和收敛性。

在另一项工作(Pawan Preet Singh 2017)中，使用SCA算法和蛾焰优化器(MFO)解决了ELD。对这些技术进行组合分析。基于正弦和余弦函数相关数学模型的概念，采用SCA进行约束优化。MFO是一种启发式算法，它利用了飞蛾向光线收敛的概念。两种算法都用于求解ELD的基准问题。组合结果表明，从所使用的各种参数来看，MFO的性能优于SCA。

Rizk M. Rizk- allah(2020)中改进的正弦余弦算法(MSCA)也用于ELD问题。在该方法中，在搜索域中初始化一组随机解，以优化环境目标和经济目标。此外，MSCA的多样性是通过对立策略来控制的。SCA的修改版本被用作具有Pareto解的多目标解决方案。提出的MSCA针对两个具有排放问题和非平稳燃料成本的实际ELD案例进行了评估。结果表明，MSCA具有较高的正确性和有效性。

在Babar等人(2020)中，使用正弦余弦算法来解决凸和非凸ELD问题。他们使用差分进化(DE)突变和交叉操作符来装备SCA。DE算法引入了SCA操作的多样性，使其避免了局部极小和过早收敛。为了保证最优的跟踪效果，提出了一种基于序列二次规划的优化算法。结果表明，与文献中报道的技术相比，这些技术在收敛时间和燃料成本方面有所改善。

摘要
1 介绍
2 生态基础 经济负荷调度问题
3.用于ELD的混合SCA
4 实验与结果
5 有限公司 结论及未来工作
参考文献
作者信息



搜索
导航

#####

在本节中，提出了针对ELD问题的带有HC优化器的混合SCA (SCA-HC)。SCA是最近的基于种群的算法，由随机解决方案的种群发起。这些解决方案迭代改进使用正弦余弦三角函数。SCA-HC有五个主要步骤，如图1中的流程图所示。在程序方面，算法1给出了SCA-HC的伪代码。

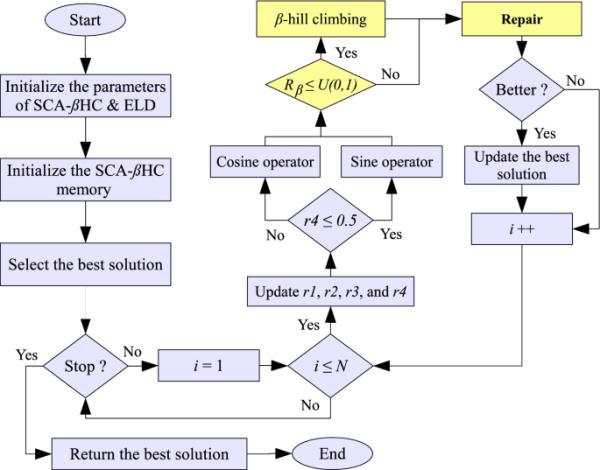
提出的SCA-HC算法流程图

• 为了使用优化方法作为SCA来解决任何优化问题，需要设计针对优化问题的建模，如目标函数和解表示。在ELD中，目标函数如式1所示。ELD解表示为一个向量，其中N是发电机组的数量。

  在SCA中，没有控制参数。然而，SCA有两个算法参数，如最大迭代次数()和种群大小(M)。对于HC优化器，有两个控制参数:和bw。负责分散搜索，而bw定义当前解与邻近解之间的距离带宽。最后，参数)决定在SCA内部调用HC优化器的速率。

• 初始化SCA-HC内存(SBM)是一个大小的矩阵，其中N为生成单元数，M为总体大小，公式为Eq.(7)。任意解的目标函数值计算公式为Eq.(1)，然后对SBM中的解按升序排序(即)。

  （7)

• 步骤3:SCA-HC进化循环这是提议的SCA-HC的进化部分。四个主要的操作符迭代到最优的ELD解决方案:(i)正弦操作符，(ii)余弦操作符，(iii)维护过程，(iv)爬坡优化器。这些操作符是连续执行的。

• 步骤3.1:正弦算子这个算子之所以叫正弦算子，是因为它使用正弦函数来更新当前的ELD解，如式(8)所示。

  （8)

• 这个算子之所以叫余弦算子，是因为它使用余弦函数来更新当前的ELD解，如式(9)所示。

  （9）

  根据其中的值，根据式(8)中的正弦函数或式(9)中的余弦函数更新当前发电单元的值，可以总结为式(10)。

  (10）

  其中为随机数。是表示下一个区域位置的参数，该区域表示解决方案与最佳解决方案之间的带宽。是表示向外或向全局最优解(或目的地)移动多远的参数。表示绘制目的地的随机权重的参数。这是为了弱化()或强调()目的地对定义的带宽距离的影响。

  任何优化算法的成功都取决于如何平衡搜索空间的探索和利用过程。因此，应使用Eq.(11)自适应地更新正弦和余弦函数之间的范围。

  (11)

• 步骤3.3:维护过程维护过程负责将不可行的解决方案修改为可行的解决方案。在调用正弦和余弦运算符之后，构造的解决方案可能是不可行的。这是因为违反了等式或不等式约束。在这种情况下，维护过程将根据允许值范围检查每个生成单元的值。此外，输出功率应等于解产生的功率。因此，维护方法如算法2所示。

  

• 步骤3.4:-爬坡优化器。爬坡优化器在SCA中充当本地搜索操作符。对于where的范围，调用-hill爬坡，如算法1所示。从正弦和余弦算子(即)构造和维护的解发生在速率范围内，被视为爬坡优化器的初始解。求解过程也使用与Eq.(1)相同的目标函数进行评估。在爬坡过程中，迭代执行三个算子进行改进:

  1. 1.

     -operator:当前解受到相邻解的影响，产生一个新的解，具体如下:其中bw是当前解与相邻解集之间的带宽，通常值较小。

  2. 2.

     -算子:在公式(12)中参数的概率范围内，使用-算子。

     （12）

     其中rnd是一个函数，生成一个在0到1之间的均匀值。任何发电机组将在其可行范围内进行再生:。

     如果生成的解决方案的可行性被破坏，SCA中使用的维护策略将再次被调用，以维护HC优化器获得的构造解决方案(算法2中的伪编码)。

  3. 3.

     -算子:当新解的目标函数值更好时，将当前解替换为新解。爬坡优化器的伪代码见算法3。

     

• 步骤4:更新SBM建议的SCA-HC在实现改进时更新其内存(SBM)。换句话说，如果新的解决方案比现有的解决方案更好，那么新的解决方案将被纳入SBM，而将被排除在外。此外，如果实现了改进，则更新最佳解决方案。

• 步骤5:终止条件当停止条件(通常取决于最大迭代次数)达到时，提议的SCA-HC被终止。到目前为止，最好的解决方案已经交付。

为了研究收敛行为，首先要对标准SCA的算子进行分析。标准SCA的算子是正弦和余弦算子。通常，收敛性分析是针对勘探开发过程进行研究的。探索指的是SCA同时导航多个搜索空间区域的能力，而利用指的是SCA收敛到每个搜索空间区域的局部最小值的能力。

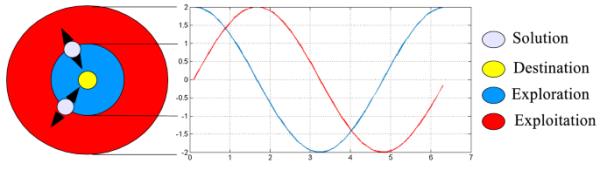
SCA中正弦收敛算子的收敛行为

正弦和余弦算子的搜索行为如图2所示。在SCA搜索期间，通过正弦或余弦运算符更新当前解决方案的位置。的值范围内，正弦余弦曲线以规则的方式移动。Mirjalili (2016b)确定了解移动的范围或(1,2)来探索搜索空间区域，而范围用于局部利用每个解的搜索空间区域。需要注意的是，在搜索过程中，正弦和余弦算子的取值范围是逐渐减小的。因此，SCA从高探索阶段开始，在运行的最后阶段向探索阶段迈进。在图2中，勘探和开发使用公式进行可视化，其中假设a为常数，t为当前迭代，而t为最大迭代次数。

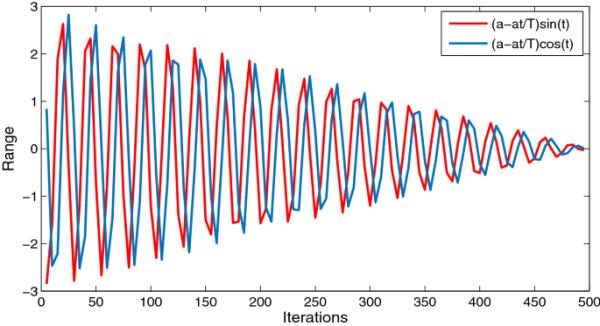
正弦余弦算法的收敛性分析

在图3中，随着迭代次数的增加，正弦和余弦方程的取值范围减小。最初，选择a的值为3，表示当前解从探索阶段移动到开发阶段的范围。可以看出，SCA的搜索过程以高搜索功率启动，在搜索过程中，搜索空间的范围逐渐退化，以识别运行的最后阶段的开发过程。因此，随着a值的增加，SCA收敛行为将在更广泛的搜索空间中启动，其中探索更加集中。搜索将缓慢地从勘探阶段移动到开发阶段，导致缓慢的收敛。反之，当a的值较小时，搜索空间的范围较窄，搜索从探索阶段快速进入开发阶段，收敛速度较快。

为了分析所提方法的时间复杂度，对算法1中的SCA-HC伪码进行了分析。最初，初始种群的生成需要时间复杂度，其中N为生成单元数，M为种群大小。在更新每个搜索代理的位置的改进循环中，第9行中的“while”循环是必需的。内部的两个“for”循环也需要时间复杂度为。算法2所示的维护(P)过程需要时间复杂度，其中dis为总负载需求与实际负载需求之间的距离带宽()。HC算法的时间复杂度等于，其中为HC算法所需的迭代次数。请注意，与SCA的原始版本相比，这是与SCA- hc相关的额外时间复杂度。

除了与所提出的SCA-HC方法的操作相关的时间复杂性外，在SCA和HC方法的每次迭代中也大量使用ELD目标函数。使用目标函数评估任何ELD解所需的时间复杂度为。

总体而言，本文提出的SCA-HC方法的时间复杂度为。显然，本文提出的SCA- hc方法的时间复杂度高于原SCA所需的时间复杂度。

在本节中，通过六个不同发电机组数量和负载需求(LD)的案例研究，测试了所提出的SCA-HC在解决ELD问题上的有效性和鲁棒性。这些情况是:

(I)案例1:3台发电机组，LD=850兆瓦;(II)案例2:6台发电机组，LD=1263兆瓦;(III)案例3:13台发电机组，LD=2520兆瓦;(IV)案例4:13台发电机组，LD=1800兆瓦;(V)案例5:15台发电机组，LD=2630兆瓦;(VI)案例6:40台发电机组，LD=10500兆瓦。

应该指出的是，在两个案例(案例2和案例5)中，在实际应用中尊重了机组的斜坡速率限制和禁区。而在其他四种情况下则考虑了阀点载荷(VPL)效应。此外，在这些情况下，传输损耗被忽略。

我们的实验是在MATLAB (R2014a)上进行的，使用英特尔(R) Core(TM) i7 2.8GHz, 16 GB RAM和操作系统管理windows 10的笔记本电脑。将所提出的SCA-HC算法的性能与现有算法进行了比较。表1显示了所有测试用例的比较算法。

为了研究不同参数设置对所提出的SCA-HC算法性能的影响，设计了14个实验场景。这些场景分为三组，如表2所示。SenExp1到SenExp4分别使用4个不同的值(=0，=0.01，=0.1，=0.5)来研究参数对SCA-HC算法性能的影响，值越大，探测率越高。接下来的五个场景(SenExp5到SenExp9)被设计用来研究参数bw对使用不同值(bw=0.001, bw=0.01, bw=0.1, bw=0.5和bw=0.95)的算法行为的影响。bw值越高，采收率越高。最后，设计了SenExp10到SenExp14这5种场景，研究了参数的影响。该参数使用以下五个不同的值进行研究:=0、=0.001、=0.01、=0.1和=0.3。的值越高，调用爬坡优化器的频率就越高，开发的频率也就越高。例如，当参数的值等于0(如SenExp10所示)时，它意味着忽略了对爬坡优化器的调用，因此在此场景中使用SCA的原始版本。为了找到所提出的SCA-HC算法的最佳配置，使用一种特设方法引入了这些设置。另一方面，其他参数的设置如下:每个实验场景的人口大小设置为30，复制运行次数也设置为30，使用的最大迭代次数为100,000。

本案例研究包括三个发电机组，三个机组的预期负荷需求为850兆瓦。单位数据取自(Walters and Sheble 1993)。表3给出了不同参数设置对所提SCA-HC算法性能影响的研究结果。在该表中，记录了每个经验场景下得到的最优方案中每个发电机组的成本。此外，最优解决方案的总成本，以及结果的均值和标准导数也总结在该表中。

SenExp1到SenExp4的设计是为了研究参数(即SenExp1 (=0)， SenExp2 (=0.01)， SenExp3(=0.1)和SenExp4(=0.5))对SCA-HC算法行为的影响。这些场景的配置如表2所示。从表3可以看出，在最佳燃料成本(即8,234.07美元/小时)方面，四种方案能够得到相同的结果。另一方面，表3中的标准导数值反映了所提出的SCA-HC算法的鲁棒性。从表3提供的结果可以看出，SenExp3中提出的SCA-HC比其他三种场景(即SenExp1、SenExp2和SenExp4)更健壮。因此，在接下来的实验中，该参数的值将被设置为0.01。

同样地，使用5种不同配置的不同场景(即SenExp5 (bw=0.001)、SenExp6 (bw=0.01)、SenExp7 (bw=0.1)、SenExp8 (bw=0.5)和SenExp9 (bw=0.95)，研究了bw参数对所提出算法性能的影响。从表3可以看出，所提出的SCA-HC在五种情况下的性能几乎是相似的，在总成本和结果的平均值方面得到了相同的结果。然而，基于标准推导结果，SenExp5的性能比其他四种场景更健壮。因此，在接下来的实验中，bw参数的值将被设置为0.001。

最后设计了5个场景(SenExp10到SenExp14)来研究参数对所提出的SCA-HC算法性能的影响。每个实验场景的具体数值分别为:SenExp10(=0)、SenExp11(=0.001)、SenExp12(=0.01)、SenExp13(=0.1)、SenExp14(=0.3)。运行这些场景的结果记录在表3中。显然，这五种方案获得了相同的最佳结果。这是因为在这种情况下所研究的问题很简单。另一方面，基于标准推导结果，本文提出的SCA-HC算法在SenExp14上的性能比其他四种场景的性能更鲁棒。

提出的SCA-HC与其他比较方法的结果记录在表4中。从表4的结果可以看出，本文算法的性能与其他15种比较方法中的13种相似，得到了最优的总燃料成本(即8,234.07美元/小时)。

在本节中，ELD问题包括6台发电机组，所有机组的期望负荷需求为1263mw。发电机组的特性见Das and Suganthan(2010)。在这种ELD问题中，考虑了单元的斜坡速率限制和禁区。表5显示了以ELD问题为例(即案例2)对所提出的SCA-HC算法的三个参数(即bw和)进行研究的结果。这些参数使用了14个实验场景进行研究。这些场景的配置如表2所示。表5记录了总燃料成本最小的最佳解决方案。此外，表5还给出了最优方案的平均成本、标准导数Stdv.、总输出功率和传输损耗。

设计了前四个实验场景(SenExp1-SenExp4)，使用4个不同的值(0、0.01、0.1和0.5)来研究参数对所提出算法性能的影响。表5总结了运行这些场景的结果。从表5可以看出，通过增加的值，所提出的SCA-HC算法的结果逐渐增强，其中最后一种场景(即SenExp4)的总燃料成本最小(即15444.43美元/小时)。因此，在本案例研究的后续实验中，该参数将被设置为0.5。

同样，SenExp5-SenExp9被设计用于研究参数bw对所提出算法行为的影响，使用这种ELD问题。值得注意的是，在这些场景中研究的bw值分别是:SenExp5 (bw=0.001)、SenExp6 (bw=0.01)、SenExp7 (bw=0.1)、SenExp8 (bw=0.5)和SenExp9 (bw=0.95)。运行这些实验场景的结果如表5所示。值得注意的是，在SenExp5场景下，该算法在总燃料成本和平均成本方面的性能优于其他四种场景。值得注意的是，这些情景的结果之间的差异不超过0.19美元/小时。这可以证明参数bw对用于此ELD情况的所提出的SCA-HC算法的行为的影响并不显著。因此，在Case 2的剩余实验中，bw参数将被设置为0.001。

最后设计了5个实验场景(SenExp10-SenExp14)来研究参数对所提出的SCA-HC算法性能的影响。使用以下值进行调查:0、0.001、0.01、0.1和0.3。需要注意的是，值越高，调用爬坡优化器的概率就越高，因此被利用的概率也就越高。从表5可以看出，随着的值的增加，本文算法的结果逐渐增强。显然，该算法在SenExp14中的性能优于其他四种场景(即SenExp10-SenExp13)，通过获得最小的总燃料成本(15444.30美元/小时)。另一方面，SenExp13与SenExp14的结果差值为0.01 $/h, SenExp12与SenExp14的结果差值为0.04 $/h。建议研究避开较大的参数值。

最后，将提出的SCA-HC的性能与其他15种比较方法进行比较，如表6所示。由表6可以看出，IGWO算法在获得最小燃料成本(15442.20 $/h)方面优于所提出的SCA-HC算法，也优于其他比较方法。而本文提出的SCA-HC算法比16种竞争方法中的11种表现更好，获得了第五好的结果(15444.30 $/h)。

13台发电机组系统由13台发电机组组成。该系统考虑了阀点效应，忽略了传输损耗。所需负荷需求为2520mw。本案例研究中各单位的数据取自(Walters and Sheble, 1993)。表7总结了使用14个实验场景研究各种参数设置对所提出的SCA-HC算法性能的结果。本表记录了运行各实验场景得到的最佳解。此外，还给出了最优解的总代价、平均代价和标准推导。应该注意的是，最好的解决方案是使用粗体突出显示。

表7显示了采用SenExp1(=0)、SenExp2(=0.01)、SenExp3(=0.1)和SenExp4(=0.5)四个不同值的实验场景，研究该参数对所提出的SCA-HC算法性能影响的结果。从表7可以看出，本文提出的SCA-HC算法在SenExp3场景下的性能优于其他三种场景，获得了最佳燃料成本(24164.12美元/小时)。这将指导我们为下一组实验设置参数为0.1。

SenExp5至SenExp9旨在研究参数bw的各种设置对SCA-HC算法行为的影响(SenExp5 (bw=0.001)， SenExp6 (bw=0.01)， SenExp7 (bw=0.1)， SenExp8 (bw=0.5)和SenExp9 (bw=0.95))。表7总结了运行这五个场景的结果。显然，SenExp7的性能优于其他四种场景，以最小的燃料成本(即27164.09美元/小时)获得最佳解决方案。在以下实验场景中，参数bw将被设置为0.1。

同样，研究不同参数值对所提SCA-HC算法性能影响的结果如表7所示。需要注意的是，该参数在5个实验场景(即SenExp10(=0)、SenExp11(=0.001)、SenExp12(=0.01)、SenExp13(=0.1)、SenExp14(=0.3))中使用5个不同的值进行研究。从7中可以看出，本文提出的SCA-HC算法在SenExp11到SenExp14中的性能优于SenExp10。这是因为参数的值被设置为零。然而，最后三种场景(即SenExp12-SenExp14)能够获得相同的最佳结果(27164.09美元/小时)。综上所述，标准推导结果表明，本文提出的SCA-HC算法在SenExp13上的性能比其他四种场景更健壮。

最后，表8显示了所提出的SCA-HC算法与其他比较方法的结果。此表中的数字代表了获得的最佳结果，以及结果的平均值。值得注意的是，所提出的SCA-HC算法的结果代表了表7中记录的最佳结果。显然，NUHS和THS算法在获得最小燃料成本(24164.06美元/小时)方面优于其他竞争方法。提出的SCA-HC算法获得了第二最小燃料成本(24164.09美元/小时)，其中SCA-HC算法与NUHS或THS算法的结果相差0.03美元/小时。此外，本文提出的SCA- hc算法的性能优于原有的自余弦算法(SCA)。

采用另一个由13台发电机组组成的测试系统对所提出的SCA-HC算法进行了测试。预计所有发电机组需要满足的负荷功率需求为1800兆瓦。本系统的发电机组数据摘自(Walters and Sheble 1993)。研究各种参数设置对所提SCA-HC算法性能影响的结果总结如表9所示。为此还设计了14个实验场景，各场景参数设置如表2所示。需要说明的是，各实验情景下总燃料成本最小的最佳解决方案记录在表9中。此外，表9总结了每个场景运行30次所获得的成本均值以及标准推导。

使用各种设置研究参数对所提出的SCA-HC算法行为的影响的结果记录在表9中。为此设计了SenExp1(=0)、SenExp2(=0.01)、SenExp3(=0.1)和SenExp4(=0.5)这四个实验场景。说明了通过运行这些场景获得的最佳结果。从表9可以看出，SCA-HC算法在SenExp3下的性能优于其他三种场景(即SenExp1、SenExp2和SenExp4)，得到最小的总燃料成本(17960.39美元/小时)。这是因为0.1的值是参数的阈值，它有助于在探索和利用之间取得适当的平衡，从而指导SCA-HC算法取得更好的结果。

接下来的5个实验场景(SenExp5-SenExp9)将使用5个不同的值(即0.001、0.01、0.1、0.5和0.95)来研究参数bw对所提出的SCA-HC算法行为的影响。表9总结了运行这些场景的结果。在该表中，记录了每种情况下得到的最优解、最优解的总燃料成本、平均成本和标准导数。从表9可以看出，本文提出的SCA-HC算法在SenExp8下的性能优于其他四种场景，得到最小的燃料成本(17960.39美元/小时)。较低的bw值会导致最差的结果，如SenExp5和SenExp6所示。此外，较高的bw值会导致最差的结果，如SenExp9所示。这证明了0.5值是参数bw的阈值，它能够在勘探和开采之间产生适当的平衡。因此，在接下来的实验中，将参数bw设为0.5。

引入最后一个实验场景(即SenExp10-SenExp14)，使用5个不同的值(即0、0.001、0.01、0.1和0.3)研究参数对所提出的SCA-HC算法性能的影响。从表9可以看出，本文提出的SCA-HC算法在SenExp12中的性能优于其他四种场景，得到最小的总燃料成本(17960.39美元/小时)。然而，本文提出的SCA-HC算法在SenExp10中的性能是最差的。这是因为参数的值等于零，因此忽略了爬坡优化器。综上所述，本文提出的SCA-HC算法以=0.1、bw=0.5、=0.01为参数设置指导，以获得本例ELD问题的最佳结果。

表10显示了SCA-HC性能与其他24种比较方法的比较。显然，所提出的SCA- hc算法的性能优于原始版本的正弦余弦算法(即SCA)。另一方面，5种竞争方法(DHS、IHS、MPDE、NUHS和THS)均能获得最小燃油成本(17960.37美元/小时)，而本文提出的SCA-HC算法能获得第三最小燃油成本(17960.39美元/小时)。值得注意的是，本文提出的SCA-HC算法的结果与其他发表的最佳结果的差异为(0.02美元/小时)。

本案例研究中考虑的ELD问题包括15个发电机组。所有机组的预期负荷需求为2630mw，所有发电机组的数据取自(Das and Suganthan 2010)。在本案例研究中考虑了单元的斜坡速率限制和禁区。表11显示了使用不同参数设置对所提出的SCA-HC算法性能的影响。采用14个实验场景对所提出的SCA-HC算法的参数进行了研究，这些场景的配置如表2所示。表11突出显示了每个实验场景中具有最小总燃料成本的最佳解决方案。此外，表11还给出了最优方案的平均成本、标准导数Stdv、总输出功率和传输损耗。最好的结果用粗体突出显示。

运行SenExp1-SenExp4的结果记录在表11中。设计这些场景来研究参数对所提出的SCA-HC算法性能的影响。从表11可以看出，本文提出的SCA-HC算法在SenExp3中的性能优于其他场景(SenExp1、SenExp2和SenExp4)，实现了最小的总燃料成本(32766.33美元/小时)。此外，SenExp1的性能比其他场景更差。这是因为该参数的值被设置为零，因此在本文算法中忽略了探索的来源。因此，在接下来的实验中使用该参数。

同样，研究bw对所提出的SCA-HC算法行为的影响的结果记录在表11中。SenExp5到SenExp9这五个实验场景就是为此而设计的。从表11中可以看出，通过获得最小的总燃料成本(32761.56美元/小时)，本文提出的SCA-HC算法在SenExp6中的性能优于其他四种场景(SenExp5, SenExp7-SenExp9)。这是为了证明0.01是参数bw的合适值，它能够在全局和局部搜索功能之间提供正确的权衡。简而言之，将在接下来的实验中用到本案例研究。

参数对所提SCA-HC算法行为影响的研究结果总结于表11。最后五个实验场景(SenExp9-SenExp14)就是为此目的而设计的。从表11可以看出，本文提出的SCA-HC算法在SenExp12中的性能优于其他四种场景，实现了最小的总燃料成本(32761.56美元/小时)。另一方面，SenExp14的性能优于其他四种场景，获得了最小的平均成本(32794.94美元/小时)。然而，最小总燃料成本将用于与文献中其他方法的比较，因此导致我们使用SenExp12获得的结果。这证明了=0.1,bw=0.01，和=0.01是所提出算法的最佳参数设置，能够在探索和利用之间取得适当的平衡，从而导航该版本ELD问题的搜索空间，从而获得更好的结果。

最后，本文提出的SCA-HC算法相对于其他14种算法获得的最佳结果如表12所示。所提出的SCA-HC算法的结果来自表11。从表12提供的结果可以看出，CS和CLCS-CLM算法能够获得相同的最佳结果(32704.45美元/小时)。另一方面，本文提出的SCA- hc算法的性能优于原始版本的SCA算法，两者之间的差异为(474.85 $/h)。此外，SCA-HC算法的性能优于CPSO、HBF、HS、IHS、PSO和PVHS算法。而所提出的SCA-HC算法的性能与其他比较算法具有一定的竞争力。

本案例研究中考虑的系统由40台具有阀点效应的发电机组组成。忽略传输损耗，期望电力负荷需求为10500 MW。本系统的发电机组数据取自(Sinha et al. 2003)。表13给出了不同参数设置对所提SCA-HC算法性能影响的研究结果。在该表中，记录了在30次重复运行中运行每个实验场景所获得的最佳解决方案。表13给出了最优方案的总燃料成本、平均成本和标准推导。各实验场景参数设置如表2所示。最佳燃料成本用粗体突出显示。

该参数在SenExp1(=0)、SenExp2(=0.01)、SenExp3(=0.1)和SenExp4(=0.5) 4种实验场景下使用4个不同的值进行研究。表13总结了这些场景运行30次以上的结果。很明显，在SenExp4中可以看出，越高的值导致结果越差，在SenExp1中忽略该参数导致结果越差。然而，本文提出的SCA-HC算法在SenExp2场景下的性能优于其他三种场景(SenExp1、SenExp3和SenExp4)，获得最小的总燃料成本(121414.70美元/小时)。另一方面，从表13的结果可以看出，与其他三种场景相比，SenExp2能够获得最小的平均成本。这证明了该参数的0.01值是该ELD问题能够在勘探和开采之间取得平衡的阈值。因此，在接下来的实验中，将使用的值。

设计了SenExp5 (bw=0.001)、SenExp6 (bw=0.01)、SenExp7 (bw=0.1)、SenExp8 (bw=0.5)和SenExp9 (bw=0.95) 5个实验场景，研究了参数bw对所提出的SCA-HC算法性能的影响。表13显示了运行这些场景的结果。从表中结果可以看出，参数bw值越高，效果越好，而SenExp8与其他4种场景(SenExp5、SenExp6、SenExp7、SenExp9)相比，总燃料成本最小，为121414.70美元/小时。另一方面，SenExp9在平均成本(121439.12美元/小时)方面产生了最好的结果。在接下来的实验中，使用，因为它可以从SenExp8中识别出最小的燃料成本。

表13显示了运行五个实验场景(即SenExp10-SenExp14)的结果，这些实验场景旨在研究参数对所提出的SCA-HC算法行为的影响。从表13可以看出，本文提出的SCA-HC算法的结果是在成本均值的基础上，通过增加的值逐渐增强的。此外，本文提出的SCA-HC算法在SenExp10 - senexp14五种场景下的性能最差，结果最差。这是因为的值等于零，因此爬坡优化器不起作用。另一方面，对于ELD问题，SenExp12比其他方案更好，因为它获得了最小的总燃料成本。综上所述，本文提出的SCA-HC的三个参数设置为=0.01、bw=0.5和=0.01时效果最佳。

最后，所提出的SCA-HC算法与其他47种比较方法的最佳结果记录在表14中。从表14可以看出，HGWO算法的性能优于所提出的SCA-HC算法，也优于其他竞争方法，获得了最小的燃料成本(121412.00 $/h)。从得到的结果来看，本文提出的SCA-HC算法排名第九(121414.70美元/小时)，其中本文提出的算法与HGWO算法的结果相差2.70美元/小时。另一方面，本文算法的性能优于原始的正弦余弦算法(SCA)，两种算法之间的差异等于3870.79美元/小时。

为了研究SCA中使用启发式搜索(即HC)的命中率，命中率参数可以考虑为。注意，此参数决定SCA命中HC的百分比。采用不同的数值对该参数进行研究，如表2所示。的不同取值得到的结果如表3、5、7、9、11、13所示。从结果可以看出，当的值越小，效果越好。因此，当来自SCA的HC的命中率较小时，由于在搜索过程中能够实现探索和利用的适当平衡，所提出的方法的行为往往更好。

图4绘制了在不同ELD问题情况下，所提出的SCA- hc算法相对于原始版本的正弦余弦算法(SCA)的收敛行为。需要注意的是，x轴表示迭代次数，y轴表示总燃料成本($/h)。为了可视化两种算法结果之间的差异，我们仔细选择了迭代次数。SCA-HC算法的参数设置是对每个ELD问题获得最小燃料成本的实验场景的设置。从图4中可以看出，SCA-HC算法在搜索过程的早期得到了接近最优的结果。此外，从图中可以看出SCA- hc算法的结果与SCA算法的结果存在较大差异，特别是在Case 3、Case 4、Case 5和Case 6中。

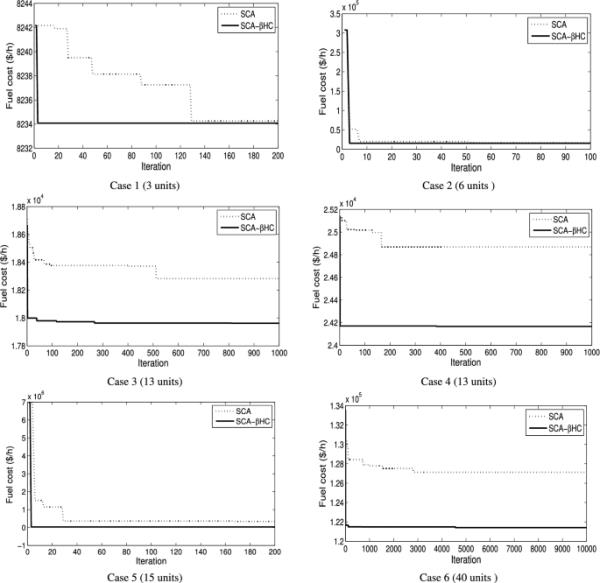
给出了不同ELD问题下SCA-HC算法的收敛图

下载原文档：https://link.springer.com/content/pdf/10.1007/s12652-022-03731-1.pdf